[ What's New ] [ Axial Ratios ] [ Unit Cell Dimensions ] [ Chemical Formula ] [ Borax Bead Tests ] [ Phosphate Bead Tests ] [ Flame Tests ] [ Cleavage ] [ Color in Minerals ] [ Chemical Composition ] [ Crystallograpic Systems ] [ New Dana Classification Number ] [ Density of Minerals ] [ Diaphaniety of Minerals ] [ Dichroism ] [ Emperical formula ] [ Environments ] [ Crystal Forms ] [ Gladstone-Dale Relationships ] [ JCrystal Applet Crystal Forms ] [ jPOWD Structure Applet ] [ jmol Structure Applet ] [ Table of Mineral Habits ] [ Mineral Hardness ] [ Magnetic Properties ] [ Mineral Tenacity and Fracture ] [ IMA status ] [ Luminescence in Minerals ] [ Mineral Luster ] [ Name Origins ] [ Name Pronunciation ] [ Optical Data ] [ Pleochroism in minerals ] [ Mineral References Cited ] [ See Also ] [ Streak colors ] [ Fermion Index ] [ Radioactivity in Minerals ] [ Reflectivity in Minerals ] [ Reflection Anisotrophism ] [ Reflected Light Bireflectance ] [ Reflected Light Color ] [ Reflection Pleochroism ] [ Locality Information ] [ Synonyms of mineral names ] [ Strunz Classification ] [ X-Ray Diffraction ]

[Mineral Specimens] [Mineral Locations] [About Us] [Search] [Register]
Greenside Minerals
Newest website on the Internet for top quality, affordable minerals from around the World
We specialize in minerals from the UK and Ireland

Optical Data

Definition

Optical Nomenclature
Gladstone-Dale
Birefringence
2V Angle
Dispersion

Optical Nomenclature used in this database.

Gladstone-Dale Relationship 

The value of the index of refraction can be calculated using chemical and physical property data if these values are missing.

The relationship between chemical composition, density, and refractive index was proposed as a means of examining gasses and solutions (Gladstone, Dale(1863), Phil. Trans, 153, 317).  This relationship is as follows:

KP = (n - 1) / d = constant 

Where

n = mean index of refraction

D = density

constant = Gladstone-Dale constant

The practice of using the Gladstone-Dale relationship to minerals only gives an approximation because of the effects that different crystal systems have on the anisotropy of the crystal lattice and the resultant values of n (index of refraction). The value of KP may be estimated from the value of Kc, the value of the Gladstone-Dale constant derived from the chemical composition.

KC = SUM OF (k1p1/100 + k2p2/100... + knpn/100). The Gladstone-Dale constant estimated from chemical analysis

Where
kc = Gladstone-Dale constant of chemical phase "n"
kp = Percentage of the chemical phase "n"

Birefringence

Birefringence is an optical property possessed by a material which has more than one index of refraction. This anisotropy in the index of refraction is dependant on the crystallographic projection and can be calculated as follows:

• Uniaxial Minerals: Birefringence = abs(NO - NE).
• Biaxial Minerals: Birefringence = NZ - NX.

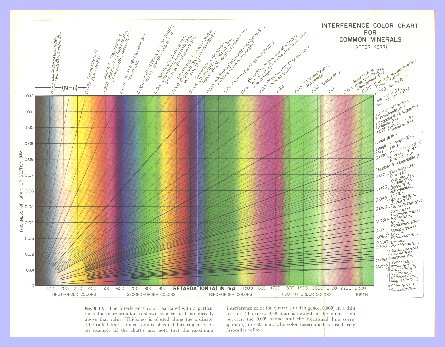
Birefringence can also be estimated from a color interference chart for colors observed under crossed polarizers on a petrographic microscope. The interference color chart is from Bloss, 1962, fig. 8-17. Click on the image for a larger picture.

Two V Calculated

TwoV(Calc) is the Biaxial 2 V angle calculated from the following relationship:

Function TwoV(A, B, C)
' From Bloss, 1962, p. 156
'
'         (gamma+beta)(gamma-beta)     alpha
'    (sqr(--------------------------)) -----  = cos(Vz)
'         (gamma+alpha)(gamma-alpha)   beta

where gamma=N_z, beta=N_y, and alpha=N_x

Dispersion

Dispersion is defined as the separation of a ray or beam of white light into its component colors. The common example is the separation due to a glass prism into the colors of the rainbow. Dispersion can be measured by calculating the index of refraction at different wavelengths. High dispersion materials separate the colors more effectively then low dispersion materials. High dispersion provides the "fire" in gemstones. Low dispersion materials are desirable in optical lenses.

In the special case of biaxial minerals, dispersion is noted by the color fringing in acute bisectrix figures using a petrographic microscope. This fringing is due to the variation of the refractive indices of α, β, and γ (Nx, Ny, Nz) with respect to wavelength. The net result is the variation of 2V angle with wavelength. This is represented by the relative position of 2Vr for red light and 2Vv for violet light on the opposite ends of the visible spectrum. This is shortened to r and v. 

• When 2Vr is less than 2Vv then it is noted as r < v.

• When 2Vr is greater than 2Vv then it is noted as r > v.

• Modifiers to r versus v include:
  none for no noticeable dispersion 
  weak for weak dispersion
  moderate for moderate dispersion
  strong for strong dispersion
  extreme for maximum dispersion

Other References to Optical Data

Search the Mineralogy Database

Example Subject Searches

Example: biaxial1.7* finds all biaxial minerals with the lowest index of refraction 1.7 to 1.79.
Example: biaxial1.7* bire=0.015* pleochroism "pale blue" finds all biaxial minerals with the lowest index of refraction from 1.7 to 1.799, a birefringence of 0.0150 to 10159 and a pale blue pleochroism.
Example: uniaxial1.6* finds all uniaxial minerals with the lowest index of refraction 1.6 to 1.69.
Example: isotropic1.5* finds all isotropic minerals with the lowest index of refraction 1.5 to 1.59.

Search the Web

	Web webmineral.com