Crystallography

Crystallography and Minerals Arranged by Crystal Form

Amorphous	Isometric	Tetragonal	Orthorhombic	Hexagonal	Trigonal	Monoclinic	Triclinic

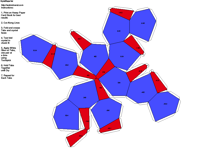
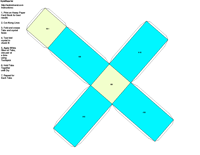
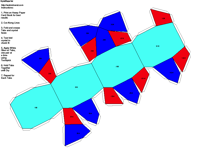
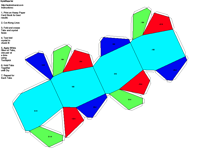
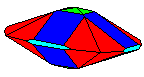
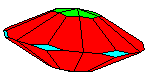
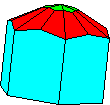
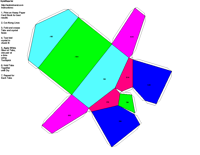
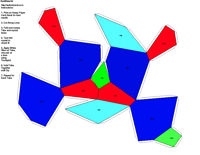
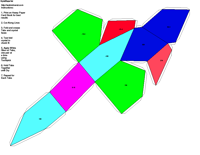
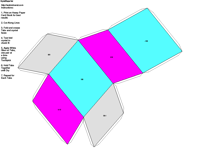
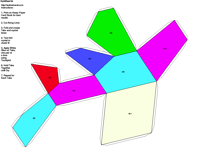
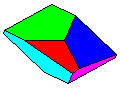
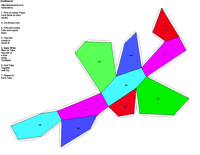
Crystal Groups and Classes - Crystallography groups are composed of 32 classes of symmetry derived from observations of the external crystal form.  From these 32 classes, 230 space groups are distinguishable using x-ray analysis.  For additional information on crystal systems, please review an excellent on-line treatment of this subject, the Introduction to Crystallography and Mineral Crystal Systems by Mike and Darcy Howard.

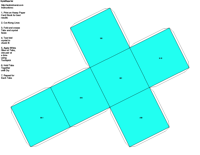
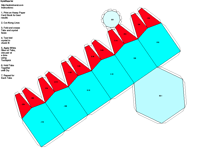
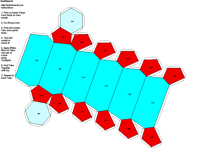
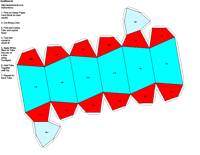
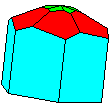
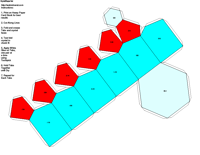
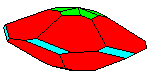
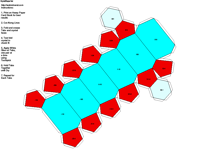
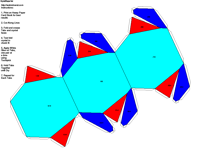
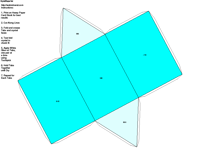
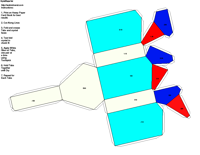
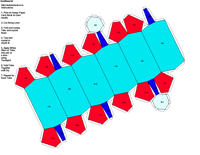
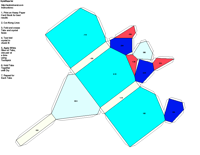
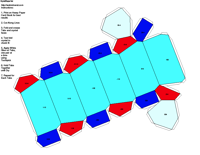
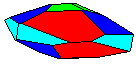
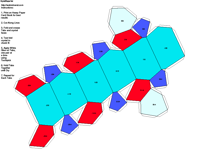
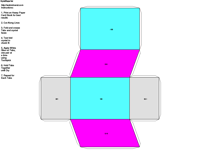
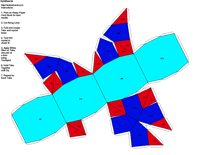
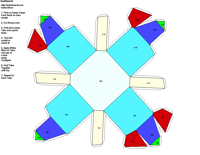
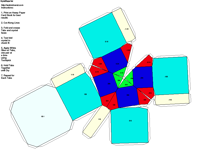
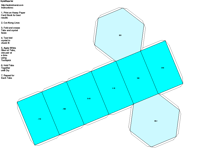
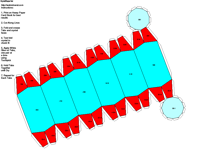
Example Crystal Morphology - To further illustrate these symmetry elements, the example crystalline forms for each symmetry class were constructed using Faces (version 3.7) by Georges Favreau for older browsers and a JAVA language program called JCrystal by Steffen Weber for the java-capable browsers. In addition, Steffen Weber has a new version of JCrystal called KrystalShaper that can produce paper models of the example crystals.    The paper models for each crystal class have been reproduced in .pdf format (see below) and can be printed on heavy card stock to construct a physical model. Please note: the paper model forms may be simplified from the JCrystal forms to avoid overly-complicated cutting.

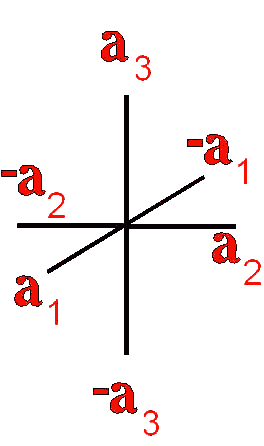
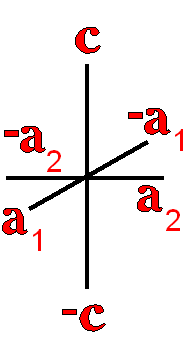
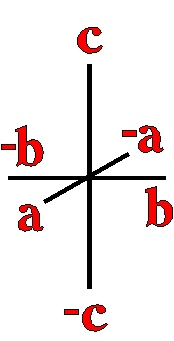
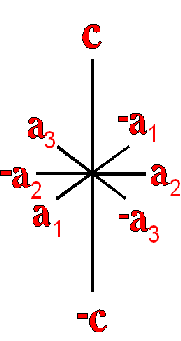
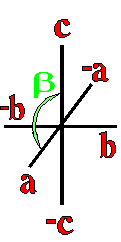
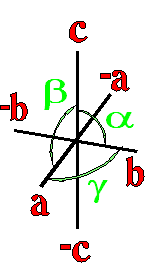
The example crystals in each group and class were constructed using the following parameters:

This morphology was used in all the crystal groups and classes for drawing the examples and the stereo images. The higher order forms were selected to best illustrate some of the subtle differences in the symmetry classes. Remember, most real crystals will probably not have similar forms when compared to the examples.

Table Crystallography (Mason 68, p18) - The thirty-two crystal classes are summarized by symmetry elements in the following table which is linked to:

ISOMETRIC - Mike and Darcy Howard's Details on The Cubic (Isometric) System

Isometric (Cubic) Crystal Classes

Crystal Axes	Example Form	Java Example Forms and Links to Mineral Listings	Paper Models
Isometric Crystallographic Axes	Isometric Minerals Crystal Form Example [214], [104], [024], [100], [010]	Class Unknown Mineral Listing
		Isometric Diploidal Mineral Listing H-M Symbol (2/m 3)
		Isometric Gyroidal Mineral Listing H-M Symbol (4 3 2)
		Isometric Hexoctahedral Mineral Listing H-M Symbol (4/m 3 2/m)
		Isometric Hextetrahedral Mineral Listing H-M Symbol (4 3m)
		Isometric Tetartoidal Mineral Listing H-M Symbol (2 3)

TETRAGONAL - Mike and Darcy Howard's Details on The Tetragonal System

Tetragonal Crystal Classes

Crystal Axes	Example Form	Java Example Forms and Links to Mineral Listings	Paper Models
Tetragonal Crystallographic Axes	Tetragonal Mineral Crystal Form Example [214], [104], [024], [100], [010]	Class Unknown Mineral Listing
		Tetragonal Dipyramidal Mineral Listing H-M Symbol (4/m)
		Tetragonal Disphenoidal Mineral Listing H-M Symbol (4)
		Tetragonal Ditetragonal Dipyramidal Mineral Listing H-M Symbol (4/m 2/m 2/m)
		Tetragonal Pyramidal Mineral Listing H-M Symbol (4)
		Tetragonal Ditetragonal-pyramidal Mineral Listing H-M Symbol (4mm)
		Tetragonal Scalenohedral Mineral Listing H-M Symbol (4 2m)
		Tetragonal Trapezohedral Mineral H-M Symbol (4 2 2)

ORTHORHOMBIC - Mike and Darcy Howard's Details on The Orthorhombic System

Orthorhombic Crystal Classes

Crystal Axes	Example Form	Java Example Forms and Links to Mineral Listings	Paper Models
Orthorhobic Crystallographic Axes	Orthorhombic Minerals Crystal Form Example [214], [104], [024], [100], [010]	Class Unknown Mineral Listing.
		Orthorhombic Dipyramidal Mineral Listing H-M Symbol (2/m 2/m 2/m)
		Orthorhombic Disphenoidal Mineral Listing H-M Symbol (2 2 2)
		Orthorhombic Pyramidal Mineral Listing H-M Symbol (mm2)

HEXAGONAL - Mike and Darcy Howard's Details on The Hexagonal System (Hexagonal Division)

Hexagonal Crystal Classes

Crystal Axes	Example Form	Java Example Forms and Links to Mineral Listings	Paper Models
Hexagonal Crystallographic Axes	Hexagonal Minerals Crystal Form Example. [214], [104], [024], [100], [010]	Class Unknown Mineral Listing.
		Hexagonal Dihexagonal Dipyramidal Mineral Listing H-M Symbol (6/m 2/m 2/m)
		Hexagonal Dihexagonal Pyramidal Mineral Listing H-M Symbol (6mm)
		Hexagonal Dipyramidal Mineral Listing H-M Symbol (6/m)
		Hexagonal Ditrigonal Dipyramidal Mineral Listing H-M Symbol (6 m2)
		Hexagonal Pyramidal Mineral Listing H-M Symbol (6)
		Hexagonal Trapezohedral Mineral Listing H-M Symbol (6 2 2)
		Hexagonal Trigonal Dipyramidal Mineral H-M Symbol (6)

TRIGONAL - Mike and Darcy Howard's Details on The Hexagonal System (Trigonal Division)

Trigonal Crystal Classes

Crystal Axes	Example Form	Java Example Forms and Links to Mineral Listings	Paper Models
Trigonal Crystallographic Axes	Trigonal Minerals Crystal Form Example. [214], [104], [024], [100], [010]	Class Unknown Mineral Listing.
		Trigonal Ditrigonal Pyramidal Mineral Listing and Stereo image. H-M Symbol (3m)
		Trigonal Hexagonal Scalenohedral Mineral Listing and Stereo image. H-M Symbol (3 2/m)
		Trigonal Pyramidal Mineral Listing and Stereo image. H-M Symbol (3)
		Trigonal Rhombohedral Mineral Listing and Stereo image. H-M Symbol ( 3)
		Trigonal Trapezohedral Mineral Listing and Stereo image. H-M Symbol (3 2)

MONOCLINIC - Mike and Darcy Howard's Details on The Monoclinic System

Monoclinic Crystal Classes

Crystal Axes	Example Form	Java Example Forms and Links to Mineral Listings	Paper Models
Monoclinic Crystallographic Axes β <> 90°	Monoclinic Minerals Crystal Form Example. [214], [104], [024], [100], [010]	Class Unknown Mineral Listing.
		Monoclinic Domatic Mineral Listing H-M Symbol (m)
		Monoclinic Prismatic Mineral Listing H-M Symbol (2/m)
		Monoclinic Sphenoidal Mineral Listing H-M Symbol (2)

TRICLINIC - Mike and Darcy Howard's Details on The Triclinic System

Triclinic Crystal Classes

Crystal Axes	Example Form	Java Example Forms and Links to Mineral Listings	Paper Models
Triclinic Crystallographic Axes α,β,γ <> 90	Triclinic Minerals Crystal Form Example. [214], [104], [024], [100], [010]	Class Unknown Mineral Listing.
		Triclinic Pedial Mineral Listing H-M Symbol (1)
		Triclinic Pinacoidal Mineral Listing H-M Symbol ( 1)